Contents
Post-Hoc Tests: Tukey, Dunnett, and Games-Howell Decision Tree
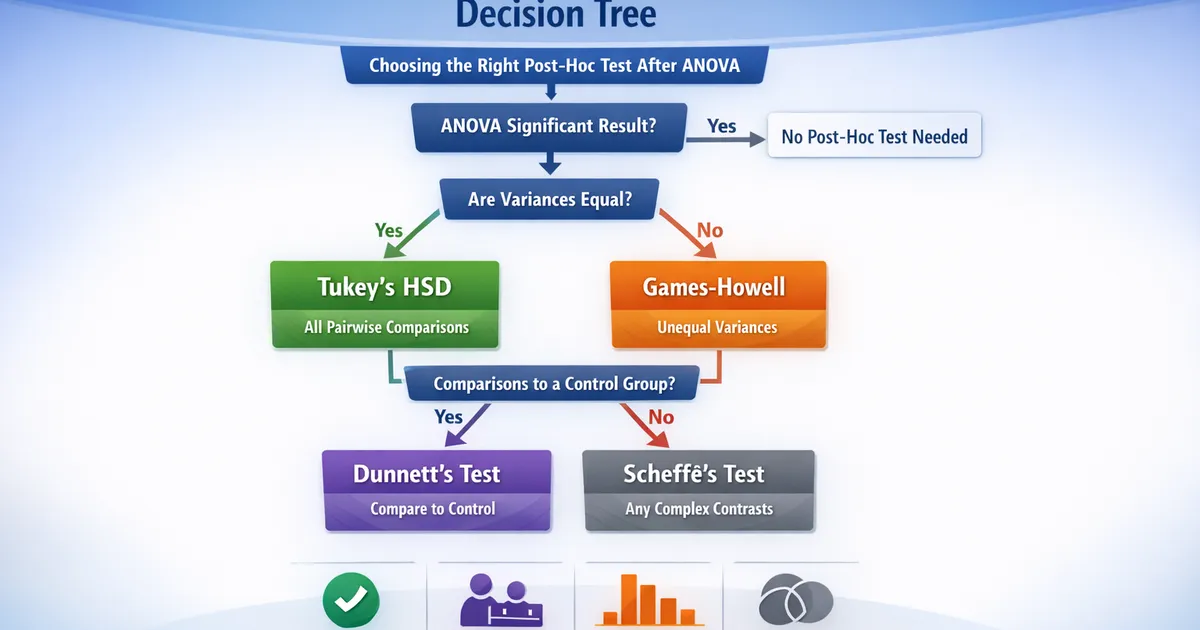
How to choose the right post-hoc test after ANOVA. Covers Tukey's HSD, Dunnett's test, Games-Howell, Scheffé, and provides a clear decision tree for selection.
Quick Hits
- •Tukey's HSD is the default for all pairwise comparisons with equal variances
- •Dunnett's is more powerful when you only care about comparisons to control
- •Games-Howell handles unequal variances and unequal sample sizes
- •Scheffé controls for ANY comparison, including complex contrasts—very conservative
TL;DR
After a significant ANOVA, post-hoc tests identify which groups differ. Tukey's HSD handles all pairwise comparisons when variances are equal. Dunnett's is more powerful when comparing treatments to a single control. Games-Howell handles unequal variances. Scheffé allows any comparison but is conservative. Choose based on your specific question and data characteristics.
The Decision Tree
Significant ANOVA → Which comparisons do you need?
│
├── Only comparing to control
│ └── Use DUNNETT'S TEST
│
├── All pairwise comparisons
│ │
│ ├── Equal variances?
│ │ ├── Yes → TUKEY'S HSD
│ │ └── No → GAMES-HOWELL
│ │
│ └── Very unequal sample sizes?
│ └── GAMES-HOWELL (safer)
│
├── Complex contrasts (not just pairs)
│ └── SCHEFFÉ
│
└── Pre-planned specific comparisons
└── BONFERRONI or HOLM (on t-tests)
Tukey's HSD (Honestly Significant Difference)
The standard choice for all pairwise comparisons with equal variances.
How It Works
Compares each pair of means using a studentized range distribution, controlling the family-wise error rate across all comparisons.
Python Implementation
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import numpy as np
import pandas as pd
def tukey_hsd(groups, group_names=None, alpha=0.05):
"""
Tukey's HSD for all pairwise comparisons.
"""
if group_names is None:
group_names = [f'Group{i+1}' for i in range(len(groups))]
all_data = np.concatenate(groups)
labels = np.repeat(group_names, [len(g) for g in groups])
result = pairwise_tukeyhsd(all_data, labels, alpha=alpha)
# Convert to dataframe for easier reading
summary_df = pd.DataFrame({
'Group 1': result._results_table.data[1:, 0],
'Group 2': result._results_table.data[1:, 1],
'Mean Diff': result._results_table.data[1:, 2],
'p-adj': result._results_table.data[1:, 3],
'Lower CI': result._results_table.data[1:, 4],
'Upper CI': result._results_table.data[1:, 5],
'Significant': result._results_table.data[1:, 6]
})
return result, summary_df
# Example
np.random.seed(42)
control = np.random.normal(50, 10, 25)
treatment_a = np.random.normal(55, 10, 25)
treatment_b = np.random.normal(52, 10, 25)
treatment_c = np.random.normal(58, 10, 25)
result, df = tukey_hsd(
[control, treatment_a, treatment_b, treatment_c],
['Control', 'Treat_A', 'Treat_B', 'Treat_C']
)
print("Tukey's HSD Results:")
print(df.to_string(index=False))
R Implementation
# After ANOVA
model <- aov(value ~ group, data = df)
TukeyHSD(model)
# Visualize
plot(TukeyHSD(model))
When to Use
- All pairwise comparisons needed
- Equal (or nearly equal) variances
- Reasonably balanced sample sizes
Dunnett's Test
Compares all treatments to a single control—more powerful than Tukey's for this specific situation.
Why More Powerful?
With k groups, Tukey's makes k(k-1)/2 comparisons. Dunnett's makes only k-1 comparisons (each treatment vs. control). Fewer comparisons = less severe correction = more power.
Python Implementation
from scipy.stats import dunnett
def dunnett_test(control, treatments, treatment_names=None):
"""
Dunnett's test: compare treatments to control.
"""
if treatment_names is None:
treatment_names = [f'Treatment{i+1}' for i in range(len(treatments))]
result = dunnett(*treatments, control=control)
summary = pd.DataFrame({
'Treatment': treatment_names,
'Statistic': result.statistic,
'p-value': result.pvalue,
'Significant': result.pvalue < 0.05
})
return result, summary
# Control vs treatments
control = np.random.normal(50, 10, 25)
treatments = [
np.random.normal(55, 10, 25),
np.random.normal(52, 10, 25),
np.random.normal(58, 10, 25)
]
result, df = dunnett_test(control, treatments, ['A', 'B', 'C'])
print("Dunnett's Test Results:")
print(df.to_string(index=False))
R Implementation
library(multcomp)
model <- aov(value ~ group, data = df)
dunnett <- glht(model, linfct = mcp(group = "Dunnett"))
summary(dunnett)
When to Use
- Comparing multiple treatments to one control
- Don't need treatment-to-treatment comparisons
- Want maximum power for your specific question
Games-Howell
For unequal variances and/or unequal sample sizes.
How It Works
Like Tukey's but doesn't assume equal variances—uses separate variance estimates for each comparison (similar to Welch's t-test).
Python Implementation
import scikit_posthocs as sp
def games_howell(groups, group_names=None):
"""
Games-Howell test for unequal variances.
"""
if group_names is None:
group_names = [f'Group{i+1}' for i in range(len(groups))]
all_data = np.concatenate(groups)
labels = np.repeat(group_names, [len(g) for g in groups])
df = pd.DataFrame({'value': all_data, 'group': labels})
result = sp.posthoc_ttest(df, val_col='value', group_col='group',
equal_var=False, p_adjust='holm')
return result
# Groups with unequal variances
group1 = np.random.normal(50, 5, 20) # SD = 5
group2 = np.random.normal(55, 15, 25) # SD = 15 (larger!)
group3 = np.random.normal(52, 10, 30) # SD = 10
result = games_howell([group1, group2, group3], ['A', 'B', 'C'])
print("Games-Howell Results (p-values):")
print(result)
R Implementation
library(rstatix)
games_howell_test(df, value ~ group)
# Or using PMCMRplus
library(PMCMRplus)
gamesHowellTest(value ~ group, data = df)
When to Use
- Levene's test shows unequal variances
- Substantially different sample sizes
- As a robust default when uncertain about variance equality
Scheffé's Test
The most conservative test—controls for ANY possible comparison, including complex contrasts.
When to Use
- You might want to test contrasts you didn't pre-specify
- Exploratory analysis where any comparison is possible
- You need maximum protection against false positives
Python Implementation
from statsmodels.stats.multicomp import MultiComparison
def scheffe_test(groups, group_names=None):
"""
Scheffé's test for post-hoc comparisons.
"""
if group_names is None:
group_names = [f'Group{i+1}' for i in range(len(groups))]
all_data = np.concatenate(groups)
labels = np.repeat(group_names, [len(g) for g in groups])
mc = MultiComparison(all_data, labels)
result = mc.allpairtest(stats.ttest_ind, method='s') # Scheffé
return result
# Note: Scheffé is very conservative for pairwise comparisons
R Implementation
library(DescTools)
ScheffeTest(model)
Warning
Scheffé is designed for post-hoc exploration of any contrast. For planned pairwise comparisons, it's overly conservative—use Tukey's instead.
Comparison Table
| Test | Best For | Assumes Equal Variance | Power | Type I Error Control |
|---|---|---|---|---|
| Tukey's HSD | All pairwise | Yes | High | FWER for all pairs |
| Dunnett's | vs. Control | Yes | Highest (for its purpose) | FWER for control comparisons |
| Games-Howell | All pairwise | No | Moderate | FWER for all pairs |
| Scheffé | Any contrast | Yes | Low | FWER for ANY comparison |
| Bonferroni | Pre-planned | Either | Varies | FWER |
Power Comparison
Same data, different tests:
def compare_posthoc_methods(groups, group_names):
"""Compare different post-hoc methods on same data."""
all_data = np.concatenate(groups)
labels = np.repeat(group_names, [len(g) for g in groups])
print("Method Comparison (adjusted p-values for A vs B):")
# Tukey's HSD
tukey = pairwise_tukeyhsd(all_data, labels)
print(f" Tukey's HSD: p = {tukey.pvalues[0]:.4f}")
# Bonferroni (manual)
from scipy.stats import ttest_ind
_, p_raw = ttest_ind(groups[0], groups[1])
n_comparisons = len(groups) * (len(groups) - 1) // 2
p_bonf = min(1, p_raw * n_comparisons)
print(f" Bonferroni: p = {p_bonf:.4f}")
# Games-Howell approximation
df = pd.DataFrame({'value': all_data, 'group': labels})
gh = sp.posthoc_ttest(df, val_col='value', group_col='group',
equal_var=False, p_adjust='holm')
print(f" Games-Howell (Holm): p = {gh.iloc[0, 1]:.4f}")
compare_posthoc_methods(
[control, treatment_a, treatment_b, treatment_c],
['Control', 'A', 'B', 'C']
)
Common Mistakes
Using Bonferroni for All Pairwise
Bonferroni is more conservative than Tukey's for pairwise comparisons. Use Tukey's instead.
Ignoring Variance Heterogeneity
If Levene's test is significant, Tukey's HSD may have inflated Type I error. Use Games-Howell.
Post-Hoc Without Significant ANOVA
Technically, if ANOVA is non-significant, you shouldn't interpret post-hoc results (though some argue for pre-planned comparisons regardless).
Using Scheffé for Simple Pairwise
Scheffé is for any possible contrast. For pairwise comparisons, it's unnecessarily conservative.
Practical Workflow
def posthoc_workflow(groups, group_names, alpha=0.05):
"""
Complete post-hoc analysis workflow.
"""
from scipy.stats import levene, f_oneway
# 1. Check ANOVA significance
f_stat, anova_p = f_oneway(*groups)
print(f"Step 1: ANOVA F = {f_stat:.2f}, p = {anova_p:.4f}")
if anova_p >= alpha:
print(" ANOVA not significant. Post-hoc not warranted.")
return None
# 2. Check variance homogeneity
levene_stat, levene_p = levene(*groups)
equal_var = levene_p > alpha
print(f"\nStep 2: Levene's test p = {levene_p:.4f}")
print(f" Variances appear {'equal' if equal_var else 'unequal'}")
# 3. Choose and run post-hoc
all_data = np.concatenate(groups)
labels = np.repeat(group_names, [len(g) for g in groups])
if equal_var:
print("\nStep 3: Using Tukey's HSD")
result = pairwise_tukeyhsd(all_data, labels, alpha=alpha)
print(result)
else:
print("\nStep 3: Using Games-Howell")
df = pd.DataFrame({'value': all_data, 'group': labels})
result = sp.posthoc_ttest(df, val_col='value', group_col='group',
equal_var=False, p_adjust='holm')
print(result)
return result
posthoc_workflow(
[control, treatment_a, treatment_b, treatment_c],
['Control', 'A', 'B', 'C']
)
Related Methods
- Comparing More Than Two Groups — The pillar guide
- One-Way ANOVA — Before post-hoc
- Heteroskedastic Groups: Games-Howell — Deep dive on unequal variances
Key Takeaway
Choose your post-hoc test based on your question: Dunnett's for comparisons to control (most powerful for that purpose), Tukey's for all pairwise comparisons with equal variances (the default), Games-Howell for unequal variances. Don't use Bonferroni for pairwise comparisons—Tukey's is specifically designed for that and is more powerful.
References
- https://www.jstor.org/stable/2685182
- https://www.jstor.org/stable/2684452
- Tukey, J. W. (1953). The problem of multiple comparisons. Unpublished manuscript, Princeton University.
- Dunnett, C. W. (1955). A multiple comparison procedure for comparing several treatments with a control. *Journal of the American Statistical Association*, 50(272), 1096-1121.
- Games, P. A., & Howell, J. F. (1976). Pairwise multiple comparison procedures with unequal n's and/or variances. *Journal of Educational Statistics*, 1(2), 113-125.
Frequently Asked Questions
Do I need post-hoc tests if ANOVA is not significant?
What's the difference between Tukey's HSD and Bonferroni?
Which test is most powerful?
Key Takeaway
Choose your post-hoc test based on your question: Dunnett's for comparisons to control, Tukey's for all pairwise comparisons with equal variances, Games-Howell for unequal variances. Don't use Bonferroni for pairwise comparisons—Tukey's is more powerful.