Contents
Comparing Retention Curves Across Segments: Multiplicity and Visualization
A practical guide to comparing survival curves across multiple segments. Learn how to visualize multiple retention curves, handle multiple comparisons, and communicate segment differences clearly.
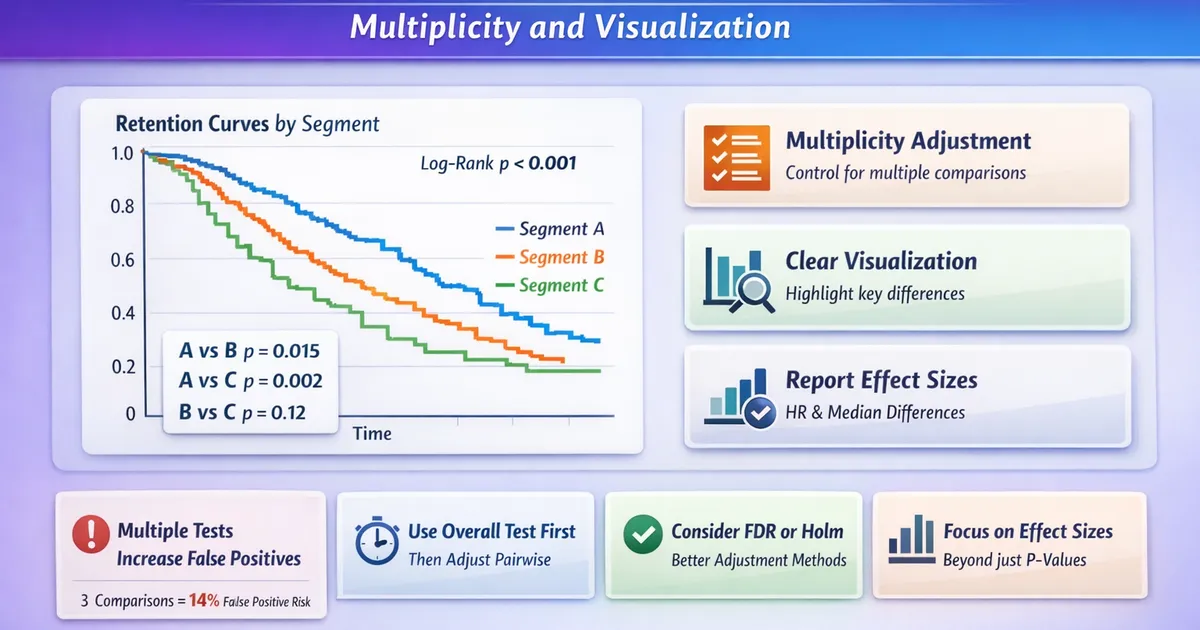
Quick Hits
- •Multiple pairwise comparisons inflate false positive rate - 3 groups = 3 tests = ~14% false positive risk
- •Use overall log-rank first, then pairwise with adjustment if significant
- •Bonferroni is conservative; Holm is better; consider FDR for exploration
- •Visualize carefully: too many curves are unreadable; use facets or highlight key comparisons
- •Report effect sizes (median difference, HR) not just p-values
TL;DR
Comparing retention curves across segments requires handling multiple comparisons properly. Testing 4 segments means 6 pairwise comparisons—without adjustment, you have a ~26% chance of at least one false positive. Use a global test first (multi-group log-rank), then pairwise comparisons with Bonferroni or Holm adjustment. For visualization, less is more: too many curves obscure patterns. Report effect sizes (median difference, hazard ratios) alongside p-values.
The Multiple Comparisons Problem
The Math
With k groups, the number of pairwise comparisons is:
| Groups | Pairwise Tests | False Positive Rate (α=0.05) |
|---|---|---|
| 2 | 1 | 5.0% |
| 3 | 3 | 14.3% |
| 4 | 6 | 26.5% |
| 5 | 10 | 40.1% |
Without adjustment, you're increasingly likely to find "significant" differences that aren't real.
Solutions
- Overall test first: Test whether any differences exist before pairwise
- P-value adjustment: Bonferroni, Holm, or FDR
- Pre-specification: Only test planned comparisons
The Two-Stage Approach
Stage 1: Overall Test
Test whether the k survival curves are all equal:
Use the multi-group log-rank test (k-1 degrees of freedom).
If : Proceed to pairwise comparisons If : Stop—no evidence of differences
Stage 2: Pairwise Comparisons with Adjustment
Compare pairs of interest with multiplicity adjustment.
P-Value Adjustment Methods
Bonferroni
Multiply p-values by number of tests (or divide α by number of tests).
Pros: Simple, controls family-wise error rate Cons: Conservative (may miss real effects)
Holm (Step-Down)
More powerful than Bonferroni while still controlling family-wise error:
- Order p-values:
- Adjusted
Pros: Uniformly more powerful than Bonferroni Cons: Slightly more complex
Benjamini-Hochberg (FDR)
Controls false discovery rate instead of family-wise error:
- Order p-values
- Adjusted
Pros: More discoveries, appropriate for exploration Cons: Accepts some false positives
Recommendation
| Goal | Method |
|---|---|
| Confirmatory (control FWER) | Holm |
| Exploratory (allow some FP) | Benjamini-Hochberg |
| Simple/conservative | Bonferroni |
| All vs. control | Dunnett |
Code: Multiple Segment Comparison
Python
import numpy as np
import pandas as pd
from lifelines import KaplanMeierFitter, CoxPHFitter
from lifelines.statistics import logrank_test, multivariate_logrank_test
from itertools import combinations
import matplotlib.pyplot as plt
def compare_multiple_segments(data, time_col, event_col, segment_col,
adjustment='holm', alpha=0.05):
"""
Compare survival curves across multiple segments with multiplicity adjustment.
Parameters:
-----------
data : pd.DataFrame
Dataset
time_col : str
Time variable
event_col : str
Event indicator
segment_col : str
Segment variable
adjustment : str
'bonferroni', 'holm', or 'fdr'
alpha : float
Significance level
Returns:
--------
dict with overall test, pairwise tests, and adjusted p-values
"""
results = {}
segments = sorted(data[segment_col].unique())
n_segments = len(segments)
# Stage 1: Overall test
overall = multivariate_logrank_test(
data[time_col],
data[segment_col],
data[event_col]
)
results['overall'] = {
'test_statistic': overall.test_statistic,
'p_value': overall.p_value,
'df': n_segments - 1,
'significant': overall.p_value < alpha
}
# Stage 2: Pairwise comparisons
pairs = list(combinations(segments, 2))
n_comparisons = len(pairs)
pairwise = []
for seg1, seg2 in pairs:
mask1 = data[segment_col] == seg1
mask2 = data[segment_col] == seg2
lr = logrank_test(
data.loc[mask1, time_col],
data.loc[mask2, time_col],
data.loc[mask1, event_col],
data.loc[mask2, event_col]
)
pairwise.append({
'segment1': seg1,
'segment2': seg2,
'test_statistic': lr.test_statistic,
'p_value': lr.p_value
})
pairwise_df = pd.DataFrame(pairwise)
# Adjust p-values
raw_p = pairwise_df['p_value'].values
if adjustment == 'bonferroni':
adj_p = np.minimum(raw_p * n_comparisons, 1.0)
elif adjustment == 'holm':
# Sort p-values
order = np.argsort(raw_p)
adj_p = np.zeros(n_comparisons)
for i, idx in enumerate(order):
multiplier = n_comparisons - i
adj_p[idx] = min(raw_p[idx] * multiplier, 1.0)
# Enforce monotonicity
sorted_adj = adj_p[order]
for i in range(1, len(sorted_adj)):
sorted_adj[i] = max(sorted_adj[i], sorted_adj[i-1])
adj_p[order] = sorted_adj
elif adjustment == 'fdr':
# Benjamini-Hochberg
order = np.argsort(raw_p)
adj_p = np.zeros(n_comparisons)
ranks = np.empty_like(order)
ranks[order] = np.arange(1, n_comparisons + 1)
adj_p = raw_p * n_comparisons / ranks
adj_p = np.minimum(adj_p, 1.0)
# Enforce monotonicity (descending in sorted order)
sorted_adj = adj_p[order[::-1]]
for i in range(1, len(sorted_adj)):
sorted_adj[i] = min(sorted_adj[i], sorted_adj[i-1])
adj_p[order[::-1]] = sorted_adj
pairwise_df['p_adjusted'] = adj_p
pairwise_df['significant'] = pairwise_df['p_adjusted'] < alpha
results['pairwise'] = pairwise_df
results['n_comparisons'] = n_comparisons
results['adjustment'] = adjustment
return results
def plot_segment_curves(data, time_col, event_col, segment_col,
title='Retention by Segment', figsize=(10, 6),
highlight=None):
"""
Plot Kaplan-Meier curves for multiple segments.
Parameters:
-----------
highlight : list, optional
Segments to highlight (others will be grayed)
"""
fig, ax = plt.subplots(figsize=figsize)
segments = sorted(data[segment_col].unique())
colors = plt.cm.tab10(np.linspace(0, 1, len(segments)))
for i, segment in enumerate(segments):
mask = data[segment_col] == segment
kmf = KaplanMeierFitter()
kmf.fit(data.loc[mask, time_col], data.loc[mask, event_col],
label=str(segment))
# Determine style
if highlight is None:
alpha = 0.8
linewidth = 2
color = colors[i]
elif segment in highlight:
alpha = 0.9
linewidth = 2.5
color = colors[i]
else:
alpha = 0.3
linewidth = 1
color = 'gray'
kmf.plot_survival_function(ax=ax, ci_show=False,
color=color, alpha=alpha,
linewidth=linewidth)
ax.set_xlabel('Time')
ax.set_ylabel('Survival Probability')
ax.set_title(title)
ax.legend(title=segment_col, loc='lower left')
ax.set_ylim(0, 1)
return fig
def create_segment_comparison_table(data, time_col, event_col, segment_col,
reference=None):
"""
Create summary table comparing segments.
"""
segments = sorted(data[segment_col].unique())
if reference is None:
reference = segments[0]
rows = []
ref_kmf = KaplanMeierFitter()
ref_mask = data[segment_col] == reference
ref_kmf.fit(data.loc[ref_mask, time_col], data.loc[ref_mask, event_col])
for segment in segments:
mask = data[segment_col] == segment
kmf = KaplanMeierFitter()
kmf.fit(data.loc[mask, time_col], data.loc[mask, event_col])
# Median survival
median = kmf.median_survival_time_
# Survival at key times
s30 = kmf.survival_function_at_times(30).values[0] if 30 <= data[time_col].max() else None
s60 = kmf.survival_function_at_times(60).values[0] if 60 <= data[time_col].max() else None
s90 = kmf.survival_function_at_times(90).values[0] if 90 <= data[time_col].max() else None
rows.append({
'Segment': segment,
'N': mask.sum(),
'Events': data.loc[mask, event_col].sum(),
'Median': median,
'D30': f"{s30:.1%}" if s30 else None,
'D60': f"{s60:.1%}" if s60 else None,
'D90': f"{s90:.1%}" if s90 else None
})
return pd.DataFrame(rows)
# Example
if __name__ == "__main__":
np.random.seed(42)
n = 800
# Generate data with 4 segments
segments = ['Basic', 'Plus', 'Premium', 'Enterprise']
hazards = {'Basic': 0.03, 'Plus': 0.02, 'Premium': 0.015, 'Enterprise': 0.01}
data = pd.DataFrame({
'segment': np.random.choice(segments, n),
})
data['time'] = data['segment'].map(lambda s: np.random.exponential(1/hazards[s]))
data['time'] = np.minimum(data['time'], 180)
data['event'] = np.random.binomial(1, 0.7, n)
# Overall and pairwise tests
results = compare_multiple_segments(data, 'time', 'event', 'segment',
adjustment='holm')
print("Segment Comparison Results")
print("=" * 60)
print(f"\nOverall Log-Rank Test:")
print(f" χ² = {results['overall']['test_statistic']:.2f}, "
f"df = {results['overall']['df']}, "
f"p = {results['overall']['p_value']:.4f}")
print(f"\nPairwise Comparisons ({results['n_comparisons']} tests, {results['adjustment']} adjustment):")
print(results['pairwise'][['segment1', 'segment2', 'p_value', 'p_adjusted', 'significant']]
.to_string(index=False))
# Summary table
print("\n" + "=" * 60)
print("Segment Summary:")
print(create_segment_comparison_table(data, 'time', 'event', 'segment').to_string(index=False))
# Plot
fig = plot_segment_curves(data, 'time', 'event', 'segment')
plt.tight_layout()
plt.show()
R
library(tidyverse)
library(survival)
library(survminer)
compare_multiple_segments <- function(data, time_col, event_col, segment_col,
adjustment = "holm") {
#' Compare survival curves with multiplicity adjustment
# Create survival object
surv_obj <- Surv(data[[time_col]], data[[event_col]])
# Overall test
formula <- as.formula(paste("surv_obj ~", segment_col))
overall_test <- survdiff(formula, data = data)
overall_p <- pchisq(overall_test$chisq, df = length(overall_test$n) - 1,
lower.tail = FALSE)
# Pairwise tests
segments <- sort(unique(data[[segment_col]]))
pairs <- combn(segments, 2, simplify = FALSE)
pairwise <- map_dfr(pairs, function(pair) {
subset <- data[data[[segment_col]] %in% pair, ]
test <- survdiff(formula, data = subset)
p <- pchisq(test$chisq, df = 1, lower.tail = FALSE)
tibble(
segment1 = pair[1],
segment2 = pair[2],
p_value = p
)
})
# Adjust p-values
pairwise$p_adjusted <- p.adjust(pairwise$p_value, method = adjustment)
pairwise$significant <- pairwise$p_adjusted < 0.05
list(
overall = list(
chisq = overall_test$chisq,
df = length(overall_test$n) - 1,
p_value = overall_p
),
pairwise = pairwise,
adjustment = adjustment
)
}
# Example
set.seed(42)
n <- 800
data <- tibble(
segment = sample(c("Basic", "Plus", "Premium", "Enterprise"), n, replace = TRUE)
) %>%
mutate(
hazard = case_when(
segment == "Basic" ~ 0.03,
segment == "Plus" ~ 0.02,
segment == "Premium" ~ 0.015,
segment == "Enterprise" ~ 0.01
),
time = rexp(n, hazard),
time = pmin(time, 180),
event = rbinom(n, 1, 0.7)
)
# Compare
results <- compare_multiple_segments(data, "time", "event", "segment")
cat("Overall Test:\n")
cat(sprintf("χ² = %.2f, df = %d, p = %.4f\n",
results$overall$chisq, results$overall$df, results$overall$p_value))
cat("\nPairwise Comparisons (Holm adjusted):\n")
print(results$pairwise)
# Plot
surv_obj <- Surv(data$time, data$event)
fit <- survfit(surv_obj ~ segment, data = data)
ggsurvplot(
fit,
data = data,
pval = TRUE,
risk.table = TRUE,
palette = "jco"
)
Visualization Best Practices
Rule 1: Limit the Number of Curves
More than 4-5 curves become hard to distinguish.
Solutions:
- Group similar segments
- Use faceted plots
- Highlight key comparisons, gray out others
Rule 2: Use Clear Color Coding
- Consistent colors across all visualizations
- Color-blind friendly palettes (avoid red-green)
- Consider using line styles for additional differentiation
Rule 3: Add Context
Include:
- Sample sizes per group
- Number of events
- Risk table (at-risk numbers over time)
- P-value from formal test
Rule 4: Focus on Practical Significance
Visual separation doesn't equal practical significance:
- Annotate key time points (D30, D90)
- Show confidence intervals
- Note absolute differences, not just visual separation
Common Mistakes
Mistake 1: Testing All Pairs Without Overall Test
Wrong: Jump straight to 6 pairwise comparisons for 4 groups.
Right: Do overall test first. If not significant, stop.
Mistake 2: Using Unadjusted P-Values
Wrong: "Segment A vs. B: " when you ran 10 tests.
Right: "Segment A vs. B: adjusted (Holm correction for 10 tests)"
Mistake 3: Over-Cluttered Visualizations
Wrong: 8 curves with confidence bands in one plot.
Right: Faceted plots, or highlight 2-3 key comparisons.
Mistake 4: Ignoring Effect Size
Wrong: "There's a significant difference ()."
Right: "Premium users have 15 days longer median retention (72 vs 57 days, )."
Related Methods
- Time-to-Event and Retention Analysis (Pillar) - Full survival framework
- Log-Rank Test - Pairwise comparisons
- Multiple Comparisons - General multiplicity guidance
- Cox Proportional Hazards - Regression for many segments
Key Takeaway
Comparing retention across multiple segments requires statistical care and visualization thoughtfulness. Use a two-stage approach: overall test first, then adjusted pairwise tests. Holm is generally preferred over Bonferroni for power. Keep visualizations simple—highlight key comparisons rather than plotting everything. Always report effect sizes (median differences, hazard ratios) alongside p-values, and remember that statistical significance doesn't equal practical importance.
References
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5506159/
- https://onlinelibrary.wiley.com/doi/10.1002/sim.5451
- https://www.nature.com/articles/s41586-019-1657-2
- Royston, P., & Parmar, M. K. (2011). The use of restricted mean survival time to estimate the treatment effect in randomized clinical trials when the proportional hazards assumption is in doubt. *Statistics in Medicine*, 30(19), 2409-2421.
- Simes, R. J. (1986). An improved Bonferroni procedure for multiple tests of significance. *Biometrika*, 73(3), 751-754.
- Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. *Journal of the Royal Statistical Society: Series B*, 57(1), 289-300.
Frequently Asked Questions
How many segments can I reasonably compare?
Do I need to adjust for multiple comparisons if I only care about one segment vs. control?
Should I adjust p-values or use a different alpha threshold?
Key Takeaway
When comparing retention across multiple segments, use an overall test first, then adjust for multiple pairwise comparisons. Visualization is as important as statistics—use clear, uncluttered plots that highlight meaningful differences. Always report effect sizes alongside p-values.