Contents
Inter-Rater Reliability: Cohen's Kappa and Krippendorff's Alpha
How to measure agreement between human raters for AI evaluation. Learn when to use Cohen's Kappa vs. Krippendorff's Alpha, how to interpret values, and what to do when agreement is low.
Quick Hits
- •Raw agreement is misleading—it doesn't account for chance agreement
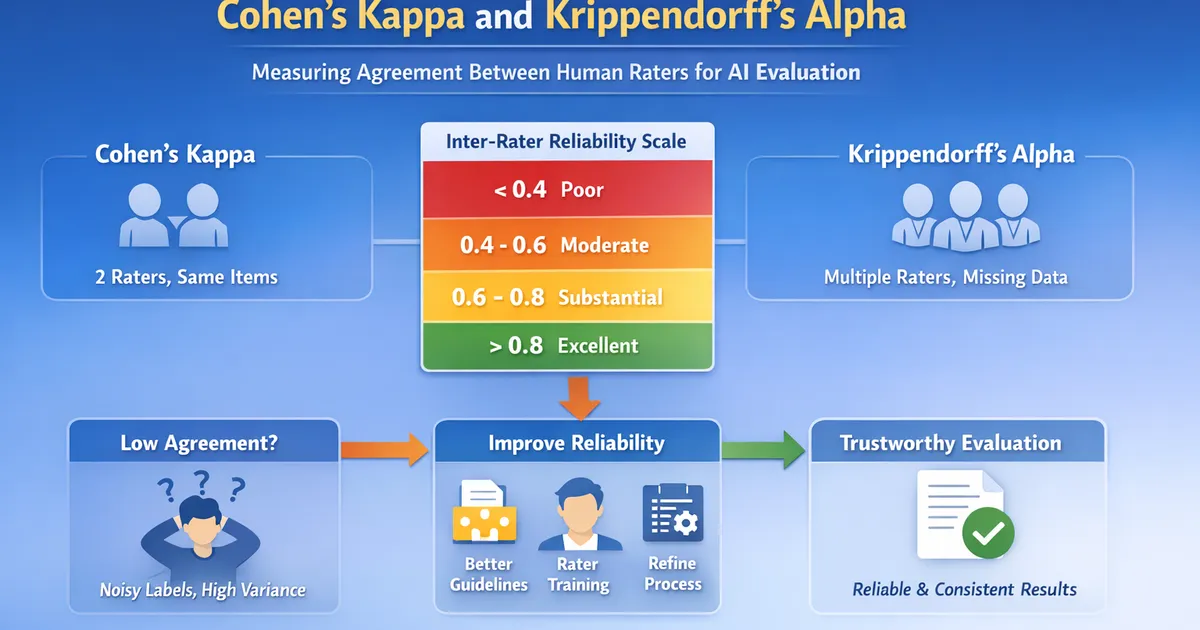
- •Cohen's Kappa: 2 raters, same items. Krippendorff's Alpha: any number of raters, handles missing data
- •Kappa < 0.4 = poor agreement, 0.4-0.6 = moderate, 0.6-0.8 = substantial, > 0.8 = excellent
- •Low agreement means noisy labels—your model evaluation will have high variance
- •Fix low agreement with better guidelines, rater training, or accepting inherent subjectivity
TL;DR
Human ratings are only useful if raters agree. Inter-rater reliability measures this agreement, correcting for chance. Cohen's Kappa works for two raters; Krippendorff's Alpha handles multiple raters and missing data. Low reliability means noisy labels and unreliable conclusions. This guide covers how to compute, interpret, and improve reliability for AI evaluation tasks.
Why Reliability Matters
The Problem with Raw Agreement
Two raters agree 85% of the time. Sounds good?
But if 90% of examples are "good" and 10% are "bad":
- Random raters agree 82% by chance (0.9² + 0.1²)
- That 85% is barely better than random
What Reliability Tells You
| Reliability | Meaning | Implication |
|---|---|---|
| High (>0.8) | Raters consistent | Labels are trustworthy |
| Moderate (0.4-0.8) | Some agreement | Labels have noise, larger samples needed |
| Low (<0.4) | Little agreement | Labels unreliable, fix process or accept subjectivity |
Cohen's Kappa
The Formula
Where:
- = observed agreement (proportion where raters agree)
- = expected agreement by chance
Implementation
import numpy as np
from collections import Counter
def cohens_kappa(rater1, rater2):
"""
Compute Cohen's Kappa for two raters.
Parameters:
-----------
rater1, rater2 : list
Ratings from each rater (same length, same items)
Returns:
--------
dict with kappa, observed/expected agreement, SE, and CI
"""
assert len(rater1) == len(rater2), "Raters must rate same items"
n = len(rater1)
# Categories
categories = sorted(set(rater1) | set(rater2))
# Observed agreement
p_o = sum(r1 == r2 for r1, r2 in zip(rater1, rater2)) / n
# Expected agreement by chance
p_e = 0
for cat in categories:
p1 = sum(r == cat for r in rater1) / n
p2 = sum(r == cat for r in rater2) / n
p_e += p1 * p2
# Kappa
if p_e == 1:
kappa = 1.0 if p_o == 1 else 0.0
else:
kappa = (p_o - p_e) / (1 - p_e)
# Standard error (large sample approximation)
se = np.sqrt((p_o * (1 - p_o)) / (n * (1 - p_e)**2))
# 95% CI
ci_lower = kappa - 1.96 * se
ci_upper = kappa + 1.96 * se
return {
'kappa': kappa,
'observed_agreement': p_o,
'expected_agreement': p_e,
'se': se,
'ci_lower': ci_lower,
'ci_upper': ci_upper,
'n': n,
'interpretation': interpret_kappa(kappa)
}
def interpret_kappa(kappa):
"""Landis & Koch interpretation."""
if kappa < 0:
return "Poor (worse than chance)"
elif kappa < 0.20:
return "Slight"
elif kappa < 0.40:
return "Fair"
elif kappa < 0.60:
return "Moderate"
elif kappa < 0.80:
return "Substantial"
else:
return "Almost perfect"
# Example: Quality ratings (bad, okay, good)
np.random.seed(42)
n = 200
# Simulate raters with moderate agreement
true_quality = np.random.choice(['bad', 'okay', 'good'], n, p=[0.2, 0.5, 0.3])
# Raters agree with truth 70% of the time
rater1 = [q if np.random.random() < 0.7 else np.random.choice(['bad', 'okay', 'good'])
for q in true_quality]
rater2 = [q if np.random.random() < 0.7 else np.random.choice(['bad', 'okay', 'good'])
for q in true_quality]
result = cohens_kappa(rater1, rater2)
print("Cohen's Kappa Analysis")
print("=" * 50)
print(f"Number of items: {result['n']}")
print(f"Observed agreement: {result['observed_agreement']:.1%}")
print(f"Expected by chance: {result['expected_agreement']:.1%}")
print(f"\nKappa: {result['kappa']:.3f}")
print(f"95% CI: ({result['ci_lower']:.3f}, {result['ci_upper']:.3f})")
print(f"Interpretation: {result['interpretation']}")
Weighted Kappa (Ordinal Data)
When categories are ordered, some disagreements are worse than others:
def weighted_kappa(rater1, rater2, weights='linear'):
"""
Weighted Cohen's Kappa for ordinal data.
weights: 'linear' or 'quadratic'
"""
# Convert to numeric
categories = sorted(set(rater1) | set(rater2))
cat_to_num = {cat: i for i, cat in enumerate(categories)}
r1_num = [cat_to_num[r] for r in rater1]
r2_num = [cat_to_num[r] for r in rater2]
n = len(rater1)
k = len(categories)
# Weight matrix
W = np.zeros((k, k))
for i in range(k):
for j in range(k):
if weights == 'linear':
W[i, j] = abs(i - j) / (k - 1) if k > 1 else 0
else: # quadratic
W[i, j] = ((i - j) / (k - 1))**2 if k > 1 else 0
# Observed agreement (weighted)
obs_counts = np.zeros((k, k))
for r1, r2 in zip(r1_num, r2_num):
obs_counts[r1, r2] += 1
obs_counts /= n
# Expected agreement (weighted)
marginals_1 = np.array([sum(r == i for r in r1_num) / n for i in range(k)])
marginals_2 = np.array([sum(r == i for r in r2_num) / n for i in range(k)])
exp_counts = np.outer(marginals_1, marginals_2)
# Weighted kappa
observed_disagreement = np.sum(W * obs_counts)
expected_disagreement = np.sum(W * exp_counts)
kappa_w = 1 - observed_disagreement / expected_disagreement if expected_disagreement > 0 else 1
return {
'weighted_kappa': kappa_w,
'weight_type': weights,
'interpretation': interpret_kappa(kappa_w)
}
# Example: 5-point scale (1=very bad to 5=very good)
np.random.seed(42)
n = 150
true_rating = np.random.randint(1, 6, n)
rater1 = np.clip(true_rating + np.random.randint(-1, 2, n), 1, 5)
rater2 = np.clip(true_rating + np.random.randint(-1, 2, n), 1, 5)
unweighted = cohens_kappa(list(rater1), list(rater2))
linear = weighted_kappa(list(rater1), list(rater2), 'linear')
quadratic = weighted_kappa(list(rater1), list(rater2), 'quadratic')
print("Weighted Kappa for Ordinal Ratings (1-5 scale)")
print("=" * 50)
print(f"Unweighted Kappa: {unweighted['kappa']:.3f}")
print(f"Linear Weighted: {linear['weighted_kappa']:.3f}")
print(f"Quadratic Weighted: {quadratic['weighted_kappa']:.3f}")
print("\nWeighted kappa is higher because it gives partial credit")
print("for 'close' disagreements (4 vs 5 is better than 1 vs 5)")
Krippendorff's Alpha
When to Use Alpha
- More than 2 raters
- Missing data (not all raters rate all items)
- Any measurement level (nominal, ordinal, interval, ratio)
Implementation
def krippendorff_alpha(data, level='nominal'):
"""
Krippendorff's Alpha for any number of raters.
Parameters:
-----------
data : array
Shape (n_raters, n_items), with np.nan for missing
level : str
'nominal', 'ordinal', or 'interval'
Returns:
--------
Alpha coefficient and interpretation
"""
data = np.array(data, dtype=float)
n_raters, n_items = data.shape
# Distance function
def distance(v1, v2, level):
if level == 'nominal':
return 0 if v1 == v2 else 1
elif level == 'interval':
return (v1 - v2) ** 2
else: # ordinal
return abs(v1 - v2)
# Observed disagreement (within items)
D_o = 0
n_pairs_obs = 0
for item in range(n_items):
ratings = data[:, item]
ratings = ratings[~np.isnan(ratings)]
if len(ratings) < 2:
continue
for i in range(len(ratings)):
for j in range(i + 1, len(ratings)):
D_o += distance(ratings[i], ratings[j], level)
n_pairs_obs += 1
if n_pairs_obs == 0:
return {'alpha': np.nan, 'error': 'Not enough overlapping ratings'}
D_o /= n_pairs_obs
# Expected disagreement (across all ratings)
all_ratings = data[~np.isnan(data)]
D_e = 0
n_pairs_exp = 0
for i in range(len(all_ratings)):
for j in range(i + 1, len(all_ratings)):
D_e += distance(all_ratings[i], all_ratings[j], level)
n_pairs_exp += 1
D_e /= n_pairs_exp if n_pairs_exp > 0 else 1
# Alpha
alpha = 1 - D_o / D_e if D_e > 0 else 1
return {
'alpha': alpha,
'observed_disagreement': D_o,
'expected_disagreement': D_e,
'level': level,
'n_items': n_items,
'n_raters': n_raters,
'interpretation': interpret_kappa(alpha)
}
# Example: 3 raters, some missing data
np.random.seed(42)
n_items = 100
n_raters = 3
# True values
true_values = np.random.choice([1, 2, 3, 4, 5], n_items)
# Raters with noise and missing data
data = np.zeros((n_raters, n_items))
for r in range(n_raters):
for i in range(n_items):
if np.random.random() < 0.9: # 10% missing
noise = np.random.choice([-1, 0, 0, 0, 1])
data[r, i] = np.clip(true_values[i] + noise, 1, 5)
else:
data[r, i] = np.nan
result = krippendorff_alpha(data, level='interval')
print("Krippendorff's Alpha Analysis")
print("=" * 50)
print(f"Raters: {result['n_raters']}")
print(f"Items: {result['n_items']}")
print(f"Measurement level: {result['level']}")
print(f"\nAlpha: {result['alpha']:.3f}")
print(f"Interpretation: {result['interpretation']}")
Diagnosing Low Agreement
Step 1: Check Category Distribution
def agreement_by_category(rater1, rater2):
"""
Break down agreement by category.
"""
categories = sorted(set(rater1) | set(rater2))
results = []
for cat in categories:
# Items where rater1 said this category
r1_cat = [i for i, r in enumerate(rater1) if r == cat]
# What did rater2 say for those items?
if r1_cat:
r2_ratings = [rater2[i] for i in r1_cat]
agree = sum(r == cat for r in r2_ratings)
results.append({
'category': cat,
'r1_count': len(r1_cat),
'agreement_when_r1': agree / len(r1_cat)
})
return results
# Example
np.random.seed(42)
n = 200
true_cat = np.random.choice(['bad', 'okay', 'good'], n, p=[0.15, 0.60, 0.25])
rater1 = [t if np.random.random() < 0.7 else np.random.choice(['bad', 'okay', 'good']) for t in true_cat]
rater2 = [t if np.random.random() < 0.6 else np.random.choice(['bad', 'okay', 'good']) for t in true_cat]
breakdown = agreement_by_category(rater1, rater2)
print("Agreement by Category")
print("=" * 50)
for row in breakdown:
print(f"{row['category']:<10} (n={row['r1_count']:<3}): {row['agreement_when_r1']:.1%} agreement")
Step 2: Find Systematic Disagreements
def confusion_matrix_raters(rater1, rater2):
"""
Confusion matrix between raters.
"""
categories = sorted(set(rater1) | set(rater2))
matrix = {c1: {c2: 0 for c2 in categories} for c1 in categories}
for r1, r2 in zip(rater1, rater2):
matrix[r1][r2] += 1
return matrix
cm = confusion_matrix_raters(rater1, rater2)
print("\nConfusion Matrix (Rater 1 rows, Rater 2 columns)")
print("=" * 50)
cats = ['bad', 'okay', 'good']
print(f"{'':>10}", end='')
for c in cats:
print(f"{c:>10}", end='')
print()
for r1 in cats:
print(f"{r1:>10}", end='')
for r2 in cats:
print(f"{cm[r1][r2]:>10}", end='')
print()
Improving Reliability
Strategy 1: Better Guidelines
## Rating Guidelines for Response Quality
### "Good" (select if ANY of these apply):
- Directly answers the question
- Provides accurate information
- Is appropriately detailed
### "Okay" (select if):
- Partially addresses the question
- Has minor errors or omissions
- Reasonable but not ideal
### "Bad" (select if ANY of these apply):
- Doesn't answer the question
- Contains significant errors
- Is confusing or unhelpful
Strategy 2: Calibration Sessions
def calibration_check(gold_labels, rater_labels):
"""
Check rater against gold standard during calibration.
"""
n = len(gold_labels)
accuracy = sum(g == r for g, r in zip(gold_labels, rater_labels)) / n
# Confusion matrix
categories = sorted(set(gold_labels))
errors = {}
for gold, rated in zip(gold_labels, rater_labels):
if gold != rated:
key = f"{gold} → {rated}"
errors[key] = errors.get(key, 0) + 1
return {
'accuracy': accuracy,
'common_errors': sorted(errors.items(), key=lambda x: -x[1])[:5]
}
# Example: Calibration feedback
gold = ['good', 'good', 'okay', 'bad', 'okay', 'good', 'okay', 'okay', 'good', 'bad']
rater = ['good', 'okay', 'okay', 'okay', 'okay', 'good', 'good', 'okay', 'good', 'bad']
result = calibration_check(gold, rater)
print("Calibration Results")
print("=" * 50)
print(f"Accuracy vs gold standard: {result['accuracy']:.1%}")
print("\nCommon errors:")
for error, count in result['common_errors']:
print(f" {error}: {count} times")
Strategy 3: Multiple Raters + Aggregation
def majority_vote(ratings):
"""Aggregate multiple raters via majority vote."""
from collections import Counter
counts = Counter(r for r in ratings if r is not None)
if counts:
return counts.most_common(1)[0][0]
return None
def agreement_with_majority(data):
"""
Measure each rater's agreement with majority.
"""
n_raters, n_items = data.shape
majorities = []
for item in range(n_items):
ratings = [data[r, item] for r in range(n_raters) if not np.isnan(data[r, item])]
majorities.append(majority_vote(ratings))
rater_agreement = []
for r in range(n_raters):
agree = sum(data[r, i] == majorities[i]
for i in range(n_items)
if not np.isnan(data[r, i]) and majorities[i] is not None)
total = sum(1 for i in range(n_items) if not np.isnan(data[r, i]))
rater_agreement.append(agree / total if total > 0 else np.nan)
return {
'rater_agreements': rater_agreement,
'mean_agreement': np.nanmean(rater_agreement)
}
R Implementation
library(irr)
# Cohen's Kappa (2 raters)
kappa2(data.frame(rater1, rater2))
# Weighted Kappa
kappa2(data.frame(rater1, rater2), weight = "squared")
# Krippendorff's Alpha (multiple raters)
kripp.alpha(t(ratings_matrix), method = "interval")
# Fleiss' Kappa (multiple raters, nominal)
kappam.fleiss(ratings_matrix)
Reporting Reliability
Template
## Inter-Rater Reliability
### Setup
- **Raters**: 3 trained annotators
- **Items**: 500 model responses
- **Rating scheme**: 3-point scale (bad, okay, good)
- **Training**: 2-hour calibration session, 50 gold-standard examples
### Results
- **Krippendorff's Alpha**: 0.67 (95% CI: 0.61-0.73)
- **Interpretation**: Substantial agreement
### Pairwise Agreement
| Pair | Kappa |
|------|-------|
| R1-R2 | 0.65 |
| R1-R3 | 0.68 |
| R2-R3 | 0.71 |
### Implications
Moderate-to-substantial agreement suggests labels are reliable
enough for comparative evaluation, though absolute quality
judgments should be interpreted with caution.
Related Methods
- Model Evaluation (Pillar) - Complete evaluation framework
- Comparing Models: Win Rate - Using ratings for comparison
- Multiple Metrics False Discoveries - Multiple testing
- Meaningful vs. Significant - Interpreting results
Key Takeaway
Human ratings are only as good as rater agreement. Measure reliability before trusting labels—Kappa and Alpha correct for chance, giving you a true measure of consistency. Low agreement (<0.4) means your labels are noisy; any conclusions drawn from them will have high uncertainty. Improve reliability through clear guidelines, calibration sessions, and rater training. When inherent subjectivity limits agreement, acknowledge this in your analysis and increase sample sizes to compensate for the noise.
References
- https://doi.org/10.1177/001316446002000104
- https://repository.upenn.edu/asc_papers/43/
- https://doi.org/10.1037/1082-989X.7.1.105
- Cohen, J. (1960). A coefficient of agreement for nominal scales. *Educational and Psychological Measurement*, 20(1), 37-46.
- Krippendorff, K. (2004). Reliability in content analysis: Some common misconceptions and recommendations. *Human Communication Research*, 30(3), 411-433.
- Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. *Biometrics*, 33(1), 159-174.
Frequently Asked Questions
What's a good Kappa/Alpha value?
Why is my Kappa low even though raters agree 80% of the time?
Which should I use: Kappa or Alpha?
Key Takeaway
Inter-rater reliability measures whether human judgments are consistent enough to trust. Kappa and Alpha correct for chance agreement, giving you a true measure of reliability. Low agreement (<0.4) means your labels are noisy—any model evaluation based on them will have high variance. Before using human ratings for evaluation, always measure and report reliability. If agreement is low, improve guidelines, add training, or acknowledge the uncertainty in your conclusions.