Contents
Comparing Two Models: Win Rate, Binomial CI, and Proper Tests
How to rigorously compare two ML models using win rate analysis. Learn about binomial confidence intervals, significance tests, and how many examples you actually need.
Quick Hits
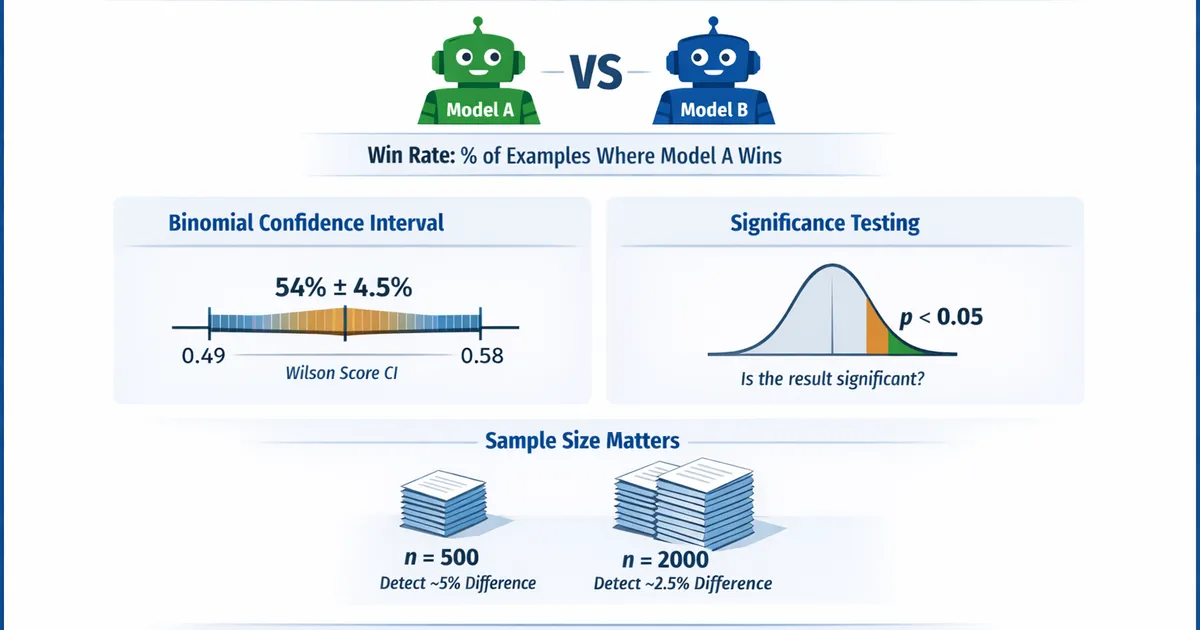
- •Win rate = proportion where Model A is better than Model B
- •54% win rate isn't necessarily different from 50%—you need a significance test
- •Wilson score CI is better than the naive formula for proportions near 0 or 1
- •Exclude ties or analyze them separately—they add noise to the comparison
- •With 500 examples, you can detect ~5% differences; with 2000, ~2.5%
TL;DR
When comparing two models, win rate (proportion of examples where A beats B) is intuitive but needs statistical treatment. A 54% win rate on 200 examples might be indistinguishable from 50% (coin flip). This guide covers proper confidence intervals for win rates, significance tests for model comparison, handling ties, and sample size requirements. The goal: make defensible claims about which model is better.
Win Rate Basics
Definition
Where "comparable" typically excludes ties.
What Win Rate Tells You
| Win Rate | Interpretation |
|---|---|
| 50% | Models equivalent |
| 55% | A is slightly better |
| 60% | A is notably better |
| 70% | A is much better |
| 80%+ | A dominates |
But these interpretations only hold if the difference is statistically significant.
Confidence Intervals for Win Rate
The Naive (Wald) Interval
Problem: Breaks down near 0% or 100%, can give impossible values (<0 or >1).
The Better Approach: Wilson Score Interval
import numpy as np
from scipy import stats
def wilson_ci(successes, n, alpha=0.05):
"""
Wilson score confidence interval for a proportion.
More accurate than Wald interval, especially for extreme p or small n.
"""
if n == 0:
return {'estimate': np.nan, 'ci_lower': np.nan, 'ci_upper': np.nan}
p_hat = successes / n
z = stats.norm.ppf(1 - alpha / 2)
denominator = 1 + z**2 / n
center = (p_hat + z**2 / (2 * n)) / denominator
margin = z * np.sqrt((p_hat * (1 - p_hat) + z**2 / (4 * n)) / n) / denominator
return {
'estimate': p_hat,
'ci_lower': max(0, center - margin),
'ci_upper': min(1, center + margin),
'method': 'Wilson score'
}
def compare_ci_methods(successes, n):
"""
Compare Wald vs Wilson confidence intervals.
"""
p_hat = successes / n
z = 1.96
# Wald (naive)
se_wald = np.sqrt(p_hat * (1 - p_hat) / n)
wald_lower = p_hat - z * se_wald
wald_upper = p_hat + z * se_wald
# Wilson
wilson = wilson_ci(successes, n)
return {
'wald': {'lower': wald_lower, 'upper': wald_upper},
'wilson': {'lower': wilson['ci_lower'], 'upper': wilson['ci_upper']}
}
# Example: Model comparison
wins_a = 270
total = 500
ties = 50
print("Win Rate Confidence Intervals")
print("=" * 50)
print(f"Model A wins: {wins_a} out of {total} non-tied comparisons")
print(f"(Plus {ties} ties excluded)")
result = wilson_ci(wins_a, total)
comparison = compare_ci_methods(wins_a, total)
print(f"\nWin Rate: {result['estimate']:.1%}")
print(f"\nWald (naive) 95% CI: ({comparison['wald']['lower']:.1%}, {comparison['wald']['upper']:.1%})")
print(f"Wilson score 95% CI: ({comparison['wilson']['lower']:.1%}, {comparison['wilson']['upper']:.1%})")
# Check if significantly different from 50%
print(f"\nCI excludes 50%: {result['ci_lower'] > 0.5 or result['ci_upper'] < 0.5}")
Significance Tests
Binomial Test (Exact)
Test H₀: win rate = 0.5 (models equally good)
def binomial_test(wins_a, wins_b, alternative='two-sided'):
"""
Exact binomial test for model comparison.
Parameters:
-----------
wins_a : int
Times Model A won
wins_b : int
Times Model B won
alternative : str
'two-sided', 'greater', or 'less'
"""
total = wins_a + wins_b
# Scipy's binomial test
p_value = stats.binom_test(wins_a, total, p=0.5, alternative=alternative)
# Effect size (difference from 50%)
win_rate = wins_a / total
effect = win_rate - 0.5
return {
'wins_a': wins_a,
'wins_b': wins_b,
'win_rate_a': win_rate,
'p_value': p_value,
'effect_size': effect,
'significant_at_05': p_value < 0.05,
'significant_at_01': p_value < 0.01
}
# Example
result = binomial_test(wins_a=285, wins_b=215)
print("Binomial Test: Is Model A Better?")
print("=" * 50)
print(f"A wins: {result['wins_a']}")
print(f"B wins: {result['wins_b']}")
print(f"A's win rate: {result['win_rate_a']:.1%}")
print(f"Effect size (vs 50%): {result['effect_size']:+.1%}")
print(f"p-value: {result['p_value']:.4f}")
print(f"Significant at α=0.05: {result['significant_at_05']}")
Z-Test (Large Sample Approximation)
Faster for large n, gives same answer as binomial test asymptotically:
def z_test_winrate(wins_a, wins_b, h0_p=0.5):
"""
Z-test approximation for win rate.
"""
total = wins_a + wins_b
p_hat = wins_a / total
# Under null
se = np.sqrt(h0_p * (1 - h0_p) / total)
z = (p_hat - h0_p) / se
p_value = 2 * (1 - stats.norm.cdf(abs(z)))
return {
'z_statistic': z,
'p_value': p_value,
'win_rate': p_hat
}
# Example
result = z_test_winrate(285, 215)
print(f"Z-test: z={result['z_statistic']:.2f}, p={result['p_value']:.4f}")
Handling Ties
Option 1: Exclude Ties (Recommended)
def analyze_with_ties(wins_a, wins_b, ties):
"""
Analyze win rate excluding ties.
"""
non_tied = wins_a + wins_b
result = {
'total_comparisons': wins_a + wins_b + ties,
'ties': ties,
'tie_rate': ties / (wins_a + wins_b + ties),
'non_tied': non_tied
}
# Win rate among non-ties
if non_tied > 0:
ci = wilson_ci(wins_a, non_tied)
test = binomial_test(wins_a, wins_b)
result.update({
'win_rate_a': wins_a / non_tied,
'ci_lower': ci['ci_lower'],
'ci_upper': ci['ci_upper'],
'p_value': test['p_value']
})
return result
# Example
result = analyze_with_ties(wins_a=230, wins_b=180, ties=90)
print("Win Rate Analysis (Excluding Ties)")
print("=" * 50)
print(f"Total comparisons: {result['total_comparisons']}")
print(f"Ties: {result['ties']} ({result['tie_rate']:.1%})")
print(f"Non-tied comparisons: {result['non_tied']}")
print(f"\nModel A win rate (among non-ties): {result['win_rate_a']:.1%}")
print(f"95% CI: ({result['ci_lower']:.1%}, {result['ci_upper']:.1%})")
print(f"p-value: {result['p_value']:.4f}")
Option 2: Bradley-Terry Model
When ties carry information (e.g., both models equally good):
def bradley_terry_with_ties(wins_a, wins_b, ties, tie_strength=0.5):
"""
Bradley-Terry model that accounts for ties.
tie_strength: how much a tie counts toward each model (0.5 = equal)
"""
# Effective wins
effective_a = wins_a + tie_strength * ties
effective_b = wins_b + tie_strength * ties
effective_total = effective_a + effective_b
# Model A's strength parameter
pi_a = effective_a / effective_total
# Standard error (approximate)
se = np.sqrt(pi_a * (1 - pi_a) / effective_total)
return {
'strength_a': pi_a,
'strength_b': 1 - pi_a,
'se': se,
'ci_lower': pi_a - 1.96 * se,
'ci_upper': pi_a + 1.96 * se
}
Sample Size Requirements
Power Analysis
def sample_size_for_winrate(effect_size, power=0.8, alpha=0.05):
"""
Calculate sample size to detect a win rate difference.
Parameters:
-----------
effect_size : float
Difference from 0.5 (e.g., 0.05 means detecting 55% vs 45%)
power : float
Desired power (default 0.8)
alpha : float
Significance level (default 0.05)
Returns:
--------
Required number of non-tied comparisons
"""
from scipy.stats import norm
p1 = 0.5 + effect_size # Win rate under alternative
p0 = 0.5 # Win rate under null
z_alpha = norm.ppf(1 - alpha / 2)
z_beta = norm.ppf(power)
# Sample size formula for one-proportion test
n = ((z_alpha * np.sqrt(p0 * (1 - p0)) +
z_beta * np.sqrt(p1 * (1 - p1))) / effect_size) ** 2
return int(np.ceil(n))
print("Sample Size Requirements for Win Rate Detection")
print("=" * 60)
print(f"{'Effect (vs 50%)':<20} {'Win Rate':<15} {'Required n':<15}")
print("-" * 60)
for effect in [0.02, 0.05, 0.08, 0.10, 0.15]:
n = sample_size_for_winrate(effect)
print(f"{effect:+.0%}{'':<17} {0.5+effect:.0%} vs {0.5-effect:.0%}{'':<8} {n:,}")
Observed Power
def observed_power(wins_a, wins_b, alpha=0.05):
"""
Calculate the power achieved with observed data.
"""
total = wins_a + wins_b
observed_rate = wins_a / total
if observed_rate == 0.5:
return 0.5 # No effect to detect
# Effect size
effect = abs(observed_rate - 0.5)
# Standard error under alternative
se_alt = np.sqrt(observed_rate * (1 - observed_rate) / total)
# Critical value under null
z_crit = stats.norm.ppf(1 - alpha / 2)
se_null = np.sqrt(0.25 / total)
# Power
if observed_rate > 0.5:
power = 1 - stats.norm.cdf(z_crit - effect / se_null)
else:
power = 1 - stats.norm.cdf(z_crit + effect / se_null)
return power
# Example
wins_a, wins_b = 270, 230
power = observed_power(wins_a, wins_b)
print(f"With {wins_a} vs {wins_b}, achieved power: {power:.1%}")
Complete Analysis Pipeline
def full_model_comparison(wins_a, wins_b, ties=0, alpha=0.05):
"""
Complete statistical analysis for model comparison.
"""
total_with_ties = wins_a + wins_b + ties
total_compared = wins_a + wins_b
# Basic stats
win_rate = wins_a / total_compared if total_compared > 0 else np.nan
# Confidence interval (Wilson)
ci = wilson_ci(wins_a, total_compared, alpha)
# Significance test
test = binomial_test(wins_a, wins_b)
# Effect size (Cohen's h for proportions)
h = 2 * np.arcsin(np.sqrt(win_rate)) - 2 * np.arcsin(np.sqrt(0.5))
# Power achieved
power = observed_power(wins_a, wins_b, alpha)
# Interpretation
if test['p_value'] < alpha:
if win_rate > 0.5:
conclusion = "Model A is significantly better"
else:
conclusion = "Model B is significantly better"
else:
conclusion = "No significant difference"
return {
'summary': {
'wins_a': wins_a,
'wins_b': wins_b,
'ties': ties,
'total': total_with_ties
},
'win_rate': {
'estimate': win_rate,
'ci_lower': ci['ci_lower'],
'ci_upper': ci['ci_upper']
},
'test': {
'p_value': test['p_value'],
'significant': test['p_value'] < alpha
},
'effect': {
'difference_from_50': win_rate - 0.5,
'cohens_h': h
},
'power': power,
'conclusion': conclusion
}
# Example
result = full_model_comparison(wins_a=285, wins_b=240, ties=75)
print("Complete Model Comparison Report")
print("=" * 60)
print(f"\nSummary:")
print(f" Model A wins: {result['summary']['wins_a']}")
print(f" Model B wins: {result['summary']['wins_b']}")
print(f" Ties (excluded): {result['summary']['ties']}")
print(f"\nWin Rate Analysis:")
print(f" A's win rate: {result['win_rate']['estimate']:.1%}")
print(f" 95% CI: ({result['win_rate']['ci_lower']:.1%}, {result['win_rate']['ci_upper']:.1%})")
print(f"\nSignificance Test:")
print(f" p-value: {result['test']['p_value']:.4f}")
print(f" Significant at α=0.05: {result['test']['significant']}")
print(f"\nEffect Size:")
print(f" Difference from 50%: {result['effect']['difference_from_50']:+.1%}")
print(f" Cohen's h: {result['effect']['cohens_h']:.3f}")
print(f"\nPower: {result['power']:.1%}")
print(f"\nConclusion: {result['conclusion']}")
R Implementation
library(binom)
# Wilson confidence interval
wilson_ci <- function(x, n, conf.level = 0.95) {
binom.confint(x, n, conf.level = conf.level, methods = "wilson")
}
# Full comparison
compare_models <- function(wins_a, wins_b, alpha = 0.05) {
n <- wins_a + wins_b
p_hat <- wins_a / n
# Wilson CI
ci <- wilson_ci(wins_a, n, 1 - alpha)
# Binomial test
test <- binom.test(wins_a, n, p = 0.5, alternative = "two.sided")
list(
win_rate = p_hat,
ci_lower = ci$lower,
ci_upper = ci$upper,
p_value = test$p.value,
significant = test$p.value < alpha
)
}
# Example
result <- compare_models(285, 240)
print(result)
Common Mistakes
Mistake 1: Ignoring Uncertainty
Wrong: "Model A wins 54% of the time" Right: "Model A wins 54% (95% CI: 49% to 59%)"
Mistake 2: Small Sample Claims
Wrong: "A beat B on 27/50 examples, so A is better" Right: "27/50 () is not significantly different from chance"
Mistake 3: Including Ties in Win Rate
Wrong: "A wins 45% (225/500), B wins 35% (175/500)" Right: "Excluding 100 ties: A wins 56% (225/400), "
Related Methods
- Model Evaluation (Pillar) - Complete evaluation framework
- Paired Evaluation: McNemar's Test - Paired comparisons
- Bootstrap for Metric Deltas - Alternative approach
- Effect Sizes for Proportions - Measuring magnitude
Key Takeaway
Win rate is the intuitive way to compare models, but raw percentages are misleading without uncertainty quantification. Always compute confidence intervals (Wilson score method), run significance tests (binomial test), and report achieved power. A 54% win rate could mean anything from "clear winner" to "random noise" depending on sample size. Plan your evaluation with power analysis: to detect a 5% difference from 50%, you need about 800 non-tied comparisons at 80% power.
References
- https://arxiv.org/abs/2303.16634
- https://aclanthology.org/2020.acl-main.442/
- https://doi.org/10.1080/00031305.1998.10480550
- Agresti, A., & Coull, B. A. (1998). Approximate is better than "exact" for interval estimation of binomial proportions. *The American Statistician*, 52(2), 119-126.
- Card, D., Henderson, P., Khandelwal, U., & Levy, R. (2020). With little power comes great responsibility. *ACL*, 3182-3193.
- Brown, L. D., Cai, T. T., & DasGupta, A. (2001). Interval estimation for a binomial proportion. *Statistical Science*, 16(2), 101-133.
Frequently Asked Questions
How do I handle ties when comparing models?
What's the minimum win rate that's meaningful?
Should I use one-sided or two-sided tests?
Key Takeaway
Comparing models via win rate requires proper statistical inference. Compute confidence intervals (Wilson score method), run significance tests (binomial or McNemar's for paired data), and determine sample size via power analysis. A 54% win rate could be noise (n=100) or definitive (n=2000). Always report the CI alongside the point estimate.