Contents
Two-Way ANOVA
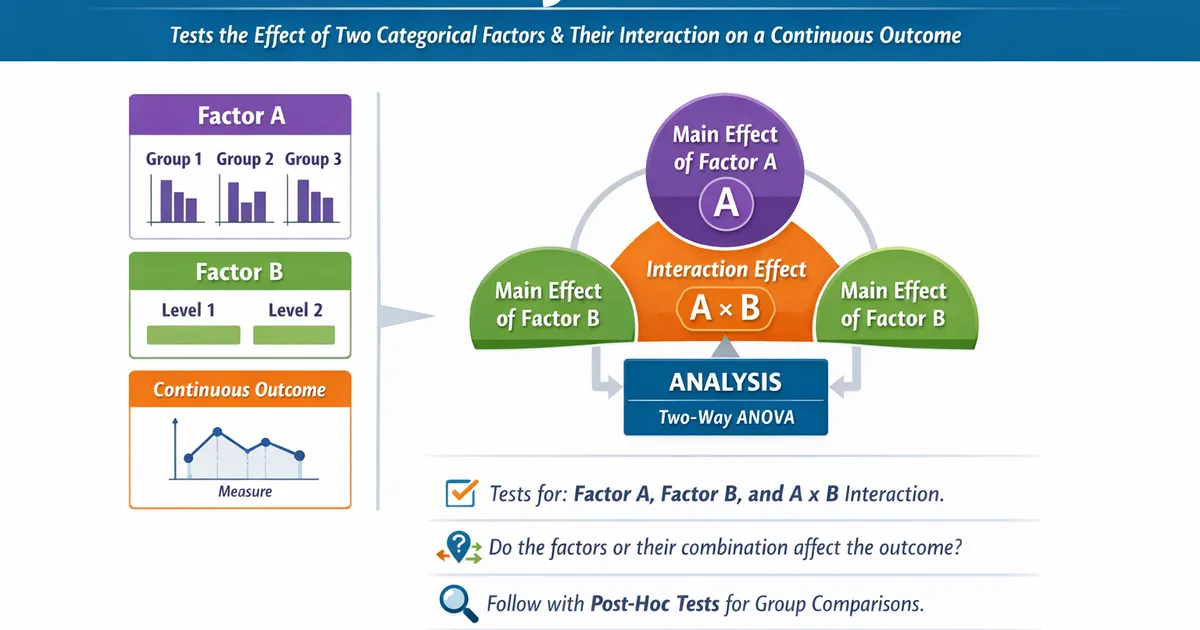
Two-Way ANOVA tests the effect of two independent factors (and their interaction) on a continuous outcome. Use it when you have two categorical grouping variables and want to know if either or both affect your outcome.
Quick Hits
- •Tests the effect of two categorical factors on a continuous outcome simultaneously
- •Decomposes variance into main effect of Factor A, main effect of Factor B, and their interaction
- •The interaction tells you whether the effect of one factor depends on the level of the other
- •Requires normally distributed data within each cell and approximately equal variances
- •Follow up with post-hoc tests (Tukey HSD) to identify which specific group pairs differ
The StatsTest Flow: Difference >> Continuous Variable of Interest >> Many Sample Tests (3+ groups) >> Two factors
Not sure this is the right statistical method? Use the Choose Your StatsTest workflow to select the right method.
What is a Two-Way ANOVA?
A Two-Way ANOVA (also called a two-factor ANOVA) is a statistical test that examines the effect of two categorical independent variables on a continuous dependent variable. It partitions the total variance in the outcome into four components: the main effect of Factor A, the main effect of Factor B, the interaction between A and B, and residual (unexplained) variance.
The interaction term is what makes a two-way ANOVA especially valuable: it tells you whether the effect of one factor changes depending on the level of the other factor.
The Two-Way ANOVA is also called a Two-Factor ANOVA, Factorial ANOVA (with 2 factors), or a Two-Way Analysis of Variance.
Assumptions for a Two-Way ANOVA
The assumptions for a Two-Way ANOVA include:
- Continuous Outcome
- Two Categorical Factors
- Normality Within Groups
- Homogeneity of Variance
- Independence
Continuous Outcome
The dependent variable must be continuous (e.g., weight, score, time, revenue).
If your outcome is categorical, consider the Chi-Square Test of Independence or Log-Linear Analysis.
Two Categorical Factors
You need exactly two grouping variables, each with two or more levels. For example, Factor A = treatment (drug, placebo) and Factor B = age group (young, middle, old).
If you have only one factor, use a One-Way ANOVA. If you have three or more factors, use a general Factorial ANOVA.
Normality Within Groups
The outcome should be approximately normally distributed within each cell (each combination of factor levels). With large sample sizes, the two-way ANOVA is robust to moderate departures from normality.
Homogeneity of Variance
The variance of the outcome should be similar across all cells. Use Levene's test to check. If violated, consider transforming the data or using a robust variant.
Independence
Observations within and across cells must be independent. If subjects appear in multiple cells (repeated measures), use a repeated-measures or mixed-design ANOVA instead.
When to use a Two-Way ANOVA?
- Your outcome is continuous
- You have two categorical grouping variables
- You want to test main effects and their interaction
- Your data is approximately normal within groups
- Groups have similar variance
Interaction is the Key Question
The primary advantage of two-way ANOVA over running two separate one-way ANOVAs is the ability to test the interaction. Does the effect of one factor depend on the other? This is often the most interesting scientific question.
Two-Way ANOVA Example
Factor A: Onboarding flow (guided wizard vs. self-serve). Factor B: User segment (individual vs. team). Outcome: Number of features activated in the first week.
We want to know whether the onboarding flow affects feature activation, whether user segment matters, and whether the best onboarding approach differs by segment.
The two-way ANOVA might reveal:
- Main effect of flow: Guided wizard leads to more features activated (F = 12.3, p < 0.001).
- Main effect of segment: Teams activate more features than individuals (F = 8.7, p = 0.004).
- Interaction: The guided wizard helps individuals much more than teams (F = 5.1, p = 0.025), who already explore features proactively.
The significant interaction means the onboarding flow matters more for individual users than for team users.
References
- https://www.statology.org/two-way-anova/
- https://online.stat.psu.edu/stat502/lesson/5
Frequently Asked Questions
What is the difference between two-way ANOVA and one-way ANOVA?
What does a significant interaction mean?
What is the difference between two-way ANOVA and factorial ANOVA?
Key Takeaway
Two-way ANOVA tests the effects of two categorical factors and their interaction on a continuous outcome. Always check the interaction first: if significant, the main effects alone do not tell the full story. Follow up with post-hoc comparisons to identify specific group differences.