σStatsTest
Login
Goodness of Fit

Kolmogorov-Smirnov Test

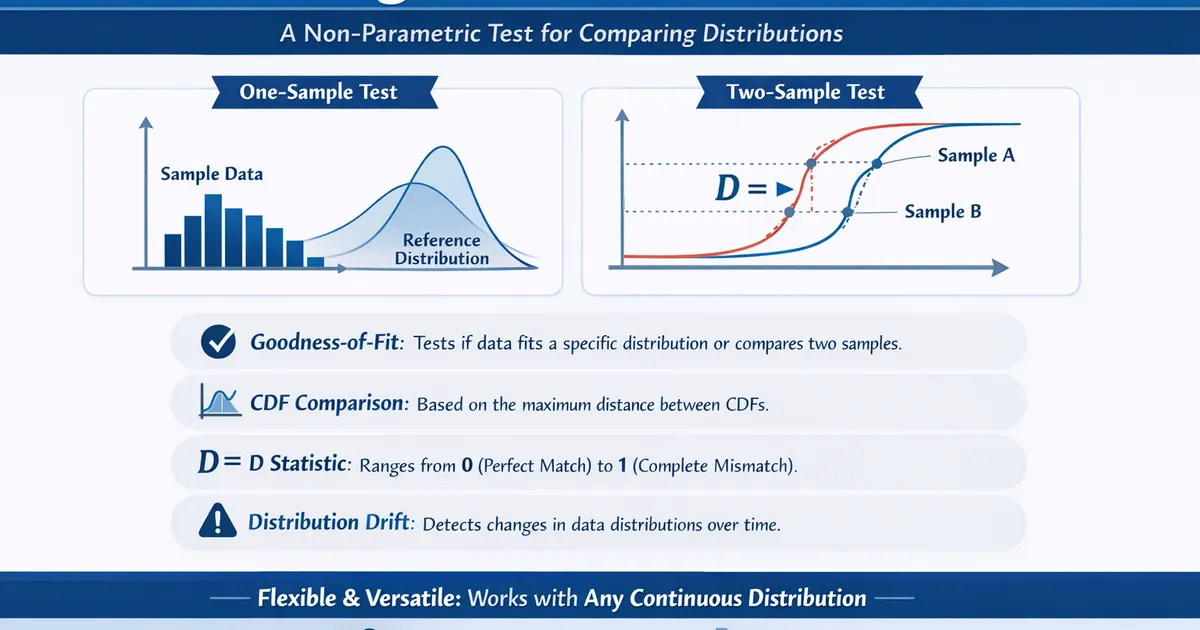
The Kolmogorov-Smirnov Test compares a sample to a reference distribution or compares two samples to each other. Use it to test goodness-of-fit to any continuous distribution or to detect distribution drift.

Jan 293 min readGoodness of FitDistribution TestNon-Parametric
Share
Kolmogorov-Smirnov Test

Quick Hits

  • •Tests whether a sample follows a specified distribution (one-sample) or whether two samples come from the same distribution (two-sample)
  • •Based on the maximum distance between cumulative distribution functions (CDFs)
  • •Non-parametric: works with any continuous distribution
  • •D statistic ranges from 0 (perfect match) to 1 (completely different)
  • •Less powerful than Shapiro-Wilk for testing normality specifically, but more flexible

The StatsTest Flow: Difference or Goodness of Fit >> Testing Distribution Assumptions >> Does my data follow a specific distribution?

Not sure this is the right statistical method? Use the Choose Your StatsTest workflow to select the right method.

What is the Kolmogorov-Smirnov Test?

The Kolmogorov-Smirnov (KS) Test is a non-parametric test that compares cumulative distribution functions (CDFs). It comes in two variants:

  1. One-sample KS test: Compares a sample's empirical CDF to a theoretical reference CDF (e.g., normal, uniform, exponential).
  2. Two-sample KS test: Compares the empirical CDFs of two independent samples to test whether they come from the same distribution.

The test statistic, D, is the maximum absolute difference between the two CDFs being compared. Larger values of D indicate greater departure from the null hypothesis.

The Kolmogorov-Smirnov Test is also called the KS Test, the Kolmogorov Test, or the Smirnov Test (two-sample version).

Assumptions for the Kolmogorov-Smirnov Test

The assumptions include:

  1. Continuous Data
  2. Independent Observations
  3. Fully Specified Reference Distribution (one-sample version)

Continuous Data

The KS test is designed for continuous distributions. For discrete data, the test is conservative (p-values are too large). Use the Chi-Square Goodness of Fit Test for categorical data.

Independent Observations

Each observation must be independent. Time-series data or clustered observations violate this assumption.

Fully Specified Reference Distribution

For the one-sample test, the reference distribution must be completely specified in advance, including all parameters. If you estimate the mean and variance from the data and then test normality against that fitted normal, the p-values will be too large. Use the Lilliefors correction or the Shapiro-Wilk Test instead.

When to use the Kolmogorov-Smirnov Test?

  1. You want to test whether your data follows a specific continuous distribution (normal, exponential, uniform, etc.)
  2. You want to compare two samples to see if they come from the same distribution
  3. You need a non-parametric, distribution-free approach
  4. You are monitoring for distribution drift over time

For normality testing specifically, the Shapiro-Wilk Test is more powerful. For comparing variances between groups, use Levene's Test.

Kolmogorov-Smirnov Test Example

Application: Monitoring model input feature distribution drift.

You deployed a machine learning model trained on data from Q3 2025. In Q1 2026, you want to check whether the distribution of the key input feature (user engagement score) has shifted.

You run a two-sample KS test comparing the Q3 2025 training distribution to the Q1 2026 production distribution. D = 0.15, p = 0.003. The significant p-value indicates the distributions have shifted, suggesting potential model degradation. You investigate and discover a UI change that increased engagement scores across the board.

References

  1. https://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
  2. https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test

Frequently Asked Questions

When should I use the KS test instead of the Shapiro-Wilk test?
Use Shapiro-Wilk when testing specifically for normality, as it is more powerful. Use the KS test when testing against any other distribution (uniform, exponential, etc.) or when comparing two empirical samples to each other.
What is the two-sample KS test used for?
The two-sample KS test compares two empirical distributions to see if they differ. Common applications include detecting data drift (has the distribution of a metric changed between two time periods?), comparing control vs. treatment distributions in experiments, or checking whether two datasets come from the same population.
What are the limitations of the KS test?
The KS test is most sensitive to differences near the center of the distribution and less sensitive to differences in the tails. It also requires a fully specified reference distribution for the one-sample test, meaning you cannot estimate parameters from the same data you are testing (use Lilliefors correction if needed). For discrete data, use an exact variant or chi-square goodness-of-fit instead.

Key Takeaway

The Kolmogorov-Smirnov test is a versatile non-parametric test for comparing distributions. The one-sample version tests whether data follows any specified continuous distribution. The two-sample version tests whether two samples come from the same distribution. It is especially useful for detecting distribution drift in monitoring and ML pipelines.

Send to a friend

Share this with someone who loves clean statistical work.

FacebookXRedditLinkedInEmail